Extracting the Private Key from a TREZOR
... with a 70 $ Oscilloscope
There were some discussions on reddit whether TREZOR, a hardware wallet for securely storing Bitcoins, can be attacked using side channels like power fluctuations, electromagnetic radiations or similar. Such an attack would allow for retrieving the private key that gives access to the Bitcoins stored on the TREZOR. Usually the discussions of side-channel attacks mention the code that signs a Bitcoin transaction. To sign a transaction on the TREZOR, you need to enter the secret PIN first. So this is not useful in the scenario where the attacker has physical access to the device but does not know the PIN.
However, also the generation of the public key may leak some information via a side channel. Until firmware 1.3.2 of TREZOR this was not PIN protected. Therefore, I investigated whether it is possible to use a side channel to recover the private key from the public key computation.
I informed Satoshi Labs of my result first, and this is why the latest firmware 1.3.3 will ask for a PIN when computing the public key. Also they included my suggested patches in this firmware that will reduce the information leaked through side-channels during computation of public keys, signatures, and decryption.
This page explains, how you can recover a private key from a TREZOR, if it still runs with firmware 1.3.1. It leaves out some crucial steps in order to make it not too simple for anyone reading this page. Nonetheless, this will hopefully give you an incentive to update your TREZOR soon. Also, if you have passphrase protection, this attack does not work even with firmware 1.3.1, so you may consider adding that, too.
The Setup
I found a cheap oscilloscope (Hantek 6022BE) for 62 EUR. (By now, the price has risen to 73 EUR at amazon). The goal was to measure power consumption of my TREZOR over time to see whether I can detect which code it is executing or even recover the private keys.
To measure the power consumption, I measured the current going through the USB cable. Since an oscilloscope can only measure voltage, I inserted a 10 Ohm resistor (for 0.05 EUR) into the mass wire of the USB cable. Thus, the voltage over this resistor is directly proportional to the current through the resistor, which is more or less proportional to the power consumption of the TREZOR.

A First Result
The above graphic shows the power consumption of a TREZOR over time on start-up. The horizontal axis is the time in seconds, the vertical axis the voltage over the resistor. The TREZOR was connected while the website mytrezor.com was open in the background. When the TREZOR is detected the PC will ask the TREZOR for the public key. If the TREZOR is not passphrase protected, it wakes up, computes the master private key from the seed and then the public key from the private key.
In the figure above, different phases can be distinguished. The regular spikes (click on the image for a larger version) are caused by the display, which runs at about 90 Hz. The power consumption of the display depends on the number of white pixels in the current line. Thus it is highest in the area where the progress bar is displayed. In the middle of the graph where the master private key is computed, you can see the spikes getting higher because the progress bar gets filled. It is also obvious where the display is swiped to the left and cleared in the process. The power consumption goes slowly down at these places.
To compute the master private key, an algorithm called PBKDF-2 is executed. During this period, the power consumption of the processor is higher than when the algorithm pauses to refresh the display (which it does eight times). After the last refresh the public key of the TREZOR is computed. When zooming close into the different parts, one can distinguish the PBKDF-2 algorithm from the part where the public key is computed.

Here we zoomed into the pbkdf-2 part of curve. This is from the first part of pbkdf, where the progressbar is not yet filled. In the middle you can see a part of lower power consumption where the function oledRefresh is called. Also you can see clearly see the regular cycle caused by the 90 Hz refresh rate of the display. Each cycle contains two spikes, which are caused by the lines above and below the progressbar. There are several small spikes, which are caused by the SHA-512 operations that the PBKDF-2 algorithm performs. The following graphic shows them in more detail.
This figure displays a single display refresh cycle, which takes about 11 milli seconds. In this graphic the individual sha-512 cycles are clearly visible except at the part where the power consumption of the display (caused by displaying the progressbar) muffles the signal of the processor.
Although the single cycles are clearly visible, they look very similar. The small distortions are probably caused by the display. It is nearly impossible to get any information about the actual values used in the SHA-512 computation. The variations in the power consumption are mainly caused by different instructions, different cache misses or branch mispredictions, instead of the different bits in the input data.
Analysing the Key Derivation Function
I was more interested in determining the private key. In this
section I will therefore look into the key generation. To avoid
noise from the display, I set a blank home screen. You can consider
this as cheating as changing the home screen requires the PIN.
However, an unscrupulous attacker may just break open the case and
rip off the display to achieve the same effect. The following
graphic shows the computation of the master
public key m/44'/0'/0'/0.
In the above graphics, there are four spikes, which mark the start of the bip32 derivation steps. If you carefully count the small spikes in between, you can determine the number of point_adds used to compute each public key. To get a feeling what goes on in this part, I put the pseudo code of the key derivation functions here.
hdnode_private_ckd_cached(HDNode *inout, int *i, int count) {
... some code looking up the key in the cache ..
for (j = 0; j < count; j++)
hdnode_private_ckd(inout, i[j])
}
hdnode_private_ckd(HDNode *inout, int i) {
... data = private/public key + i ...
I = hmac_sha512(inout->chaincode, data)
inout->chaincode = I[32:]
inout->private_key += I[0:32];
inout->public_key = scalar_multiply(inout->private_key)
}
// compute point private_key * G.
scalar_multiply(bignum256 *private_key) {
iszero = 1
for (int i = 0; i < 255; i++) {
if (privatekey & (1 << i)) {
// do two bits at a time.
twobits = (privatekey >> i) & 3;
// lookup twobits * 2 ^ i * G in a big table.
toadd = bigtable[twobits][i];
if (iszero) {
res = toadd;
iszero = 0;
} else {
res = point_add(res, toadd);
}
i++; // skip another bit
}
}
return res;
}
point_add(point *a, point *b) {
... some conditons that are usually false ...
bn_inverse(b->x - a->x);
... some multiplications ...
}
bn_inverse(bignum256 *a) {
... some talkative function leaking
a lot of random information about the
input a over my side-channel ...
}
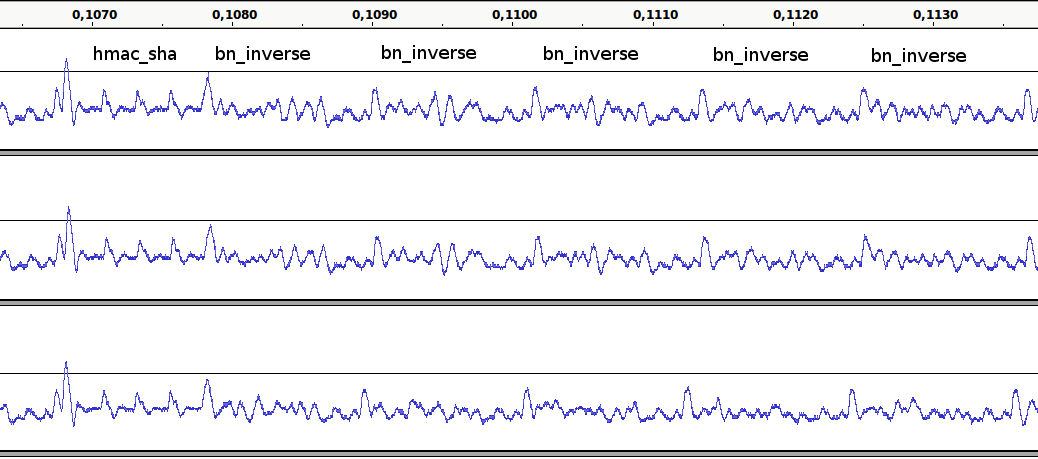
The following graphic shows the first part of a key derivation steps in more detail and compares different runs of the algorithm.
The first and second row show the computation of a public key for
the same private key in two different runs. The third row shows a
computation of a public key for a different private key. You can
clearly see the SHA-512 cycles at the beginning that we already have
seen in the zoomed in part of the pbkdf-2 algorithm. These are
needed by the BIP32 algorithm to compute the child private key.
After these cycles, the computation of the public key begins. To
compute the public key, the function scalar_multiply
calls the function point_add for each one bit occurring in
the private key. You can see the start of this part by a small
spike. Most time of the point addition is taken by the
function bn_inverse. This is a particularly
interesting function, since the code it is executing is dependent on
the input and it looks different for every input, with which it is
called. You can see that it produces are random looking pattern.
In the end there are a few multiplications, that will again form two
regular small spikes followed by a big spike, where the next point
addition starts.
If you compare the three rows, you can see that the pattern
caused by the function bn_inverse looks very
different each round, but is the same if it is called on the same
input, as it is done in the first and second row.
How to Recover the Private Key
One can clearly see the one bits in the private key, as these cause the point addition to be called, which is clearly visible. I hoped that one could see the zero bits in the private key that are skipped by scalar_multiply. However, the time these operations take is too short to be visible. So the direct approach to read the bits from the wave does not work.
However, the input dependent
fingerprint of the bn_inverse function is enough
to recover the private key.
The idea is that the input of the first bn_inverse
function depends only on the first two points added in
the scalar_multiply loop. At this time the function will
have processed only a few of the lowest bits of the private key.
One can generate all the possible values for the lowest bits
of the key, compute the corresponding public keys on a reference TREZOR,
and record the fingerprints of bn_inverse.
These can be compared with the fingerprints of the
victim TREZOR. On average one has to check 26.5 fingerprints until
one finds a matching fingerprint and thus the lowest bits. The later
steps get even easier; for them only 5.5 fingerprints have to be checked
on average.
I have recovered 128 bits of a private key as a proof of concept.
It took me about two hours and it would take the same time to
recover the second half. The main problem is that one needs a
reference TREZOR and use it to retrieve the necessary fingerprints
of the bn_inverse functions. This work has to be
repeated for every private key.
There is no need to have extended access to the TREZOR you want to break. A simple recording of one key derivation (which can be done in a few seconds) give you all the information you need from this TREZOR. The exact fingerprint depends on the exact firmware, though. I guess that the alignment of the function is important, i.e., whether it crosses a cache line. However, the fingerprint is close enough to recognise it, even if the firmware is different.
Improvements to Firmware
In reaction to these results, PIN protection was added for computing public keys. This should prevent most side-channel attacks.
Furthermore, I suggested a few improvements to the firmware that
should remedy this problem.
The first
improvement was only planned to give a slightly better
performance to the bn_inverse function; not even
removing the input dependent timing. Nonetheless, it made the
function completely invisible for my oscilloscope. Why did this happen?
My best guess is that because I removed some duplicated code, the same
code path is used throughout the inner loop, while the previous
code switched between the u is even and v is even code
paths, depending on the input.
However, the exact timing of the function still depends on the input.
Therefore, it may still be possible to recover the private key by
observing the duration of each point_add.
This segment starts when the get_public_node package
has just been received. At the beginning there is again the
HMAC-SHA256 computation. As you can see the calls
to bn_inverse produce an almost flat signal. The peaks
are caused by the final multiplications
in point_add.
The second
patch set gives almost constant time to
the scalar_multiply function. The only input dependent
timing is in a final bn_inverse call that is randomised
and is only called at the very end, when the full key has been
processed. This should make it impossible to recover any
information about the private key. Another side-effect of this
patch is that the signal is even more silent.
This segment starts near the end of
a scalar_multiply call. You can see four calls of
point_jacobian_add followed by bn_inverse
called from jacobian_to_point. Then the next public
key is derived and there is again an application of HMAC-SHA256.
After a point_to_jacobian there follows the regular
sequence of point_jacobian_add.
There is still a table look-up for the point
in scalar_multiply and I'm not sure if this makes
problems. In principle by detecting cache misses one could get some
information about the private keys. However, I could not detect a
difference between cache hit or miss with my hardware.
Although the code is not perfect, it should make side-channel
attacks much more difficult. With my technique (checking the power
consumption at the USB cable), I cannot see any way to recover the
private key from a side channel attack
on scalar_multiply. Also analysing electromagnetic
radiation or acoustics shouldn't be feasible, as they have even less
information. It may be possible to recover more information by
opening the device and measuring the power consumption directly at
the processor. This requires physical access and in that case you
now need the PIN for every operation.
Downloads
I put some recordings into a zip file recordings.zip. These are uncompressed wav files. I found it most convenient to look at them with audacity. The graphics above were all created with this program. The zip file contains (1) a full recording of the initial sequence for both the default home screen and a blank one, (2) the recording of the bip32 phase only, using a higher sampling frequency, (3) the recording of the bip32 phase with blank home screen using a firmware with the branch bignum_improvements. In principle it should be possible to extract the private key from this data. I think there are even some Test coins protected by these keys, so have fun with them, if you recover the key :)Time-line
- 2015-03-21: firmware 1.3.2 was tagged.
- 2015-03-24: firmware 1.3.2 binary added to webwallet-data repository, but not yet published.
- 2015-03-24: my oscilloscope arrived. In anticipation I had everything prepared.
- 2015-03-26: first results. I informed stick and slush at that time. They asked to delay publication until they can resolve the issues in a new firmware release 1.3.3.
- 2015-03-29: I managed to extract a big part of a private key by applying the technique sketched above.
- 2015-03-30: PIN protection added to firmware code. My patches to the relevant cryptographic functions were merged into the TREZOR repository.
- 2015-04-07: firmware 1.3.3 released.
- 2015-04-09: this page was published.
Conclusion
Side channel attacks are not as difficult as many people think. A simple power analysis requires only a simple oscilloscope and that can hardly be called expensive laboratory equipment. You also need basic soldering skills and deep knowledge about the code that is running. It took only a single recording of the computation of the public key, to recover the private key. On the bright side, this simple side channel attack can be mitigated by using constant-time code and as I showed this code does not have to be slow.
The new firmware 1.3.3 is immune against this attack since it (1) requires a PIN to compute the public key and (2) uses branch-free computations for deriving the public key from the private key.
There is no complete protection against all kind of attacks. If your TREZOR gets stolen and it has no passphrase protection (or if the passphrase is weak), you should transfer the coins to a different wallet. There are other attack vectors like fault injection that could still be used and may get around the PIN protection. Basically, they use the fact that the microprocessor does unexpected things if power supply or the clock signal is broken. These are much more difficult to perform, but they are probably less expensive than using an electron microscope to read the seed from the chip. Also, there may be a bug in the microprocessor that allows for circumventing the read-out protection.
Disclaimer
At the time I did this work, I was not involved with Satoshi Labs or any of their competitors. I own two TREZORs myself and I am still thinking hardware wallets are the best way to protect against most attack vectors. Problems like this are to be expected in any new product and TREZOR is barely a year old now. It is more important that these things get fixed in a timely manner.
If you want to support my work, you can send bitcoins to bc1q9yzrukhrlz0chfjzhr0gd7g3l6aah22xlqjuhl